TL;DR: “Greedy probing works — until it doesn’t. This post shows how a small shift in fallback strategy, Elastic Rotation, turns sudden failure into gradual degradation. We break the cliff, bend the curve, and rethink what fairness really means under pressure.”
Greedy: Elegant Until Everyone’s Circling
Think of a hash table like a car park.
Each slot is a parking bay. Each key is a driver. And the hash function? That’s the parking attendant pointing them to their first choice.
And if that bay’s taken? The attendant hands over a list of backup instructions — “Try the next one along, then the next…”
Greedy probing feels like the perfect plan: hash the key, find the next empty bay, park the car. Simple. Fast. Done.
It’s elegant in its simplicity — and for a while, it works flawlessly.
At 50% full, it’s easy to find a spot.
Even at 75%, you’re still gliding in without much fuss.
But as the car park fills into the high 90s, that easy parking turns into chaos.
Every insert becomes a slow lap. Every fallback instruction takes you further from the entrance.
You’re not inserting — you’re circling the block.
Here’s what that collapse looks like:
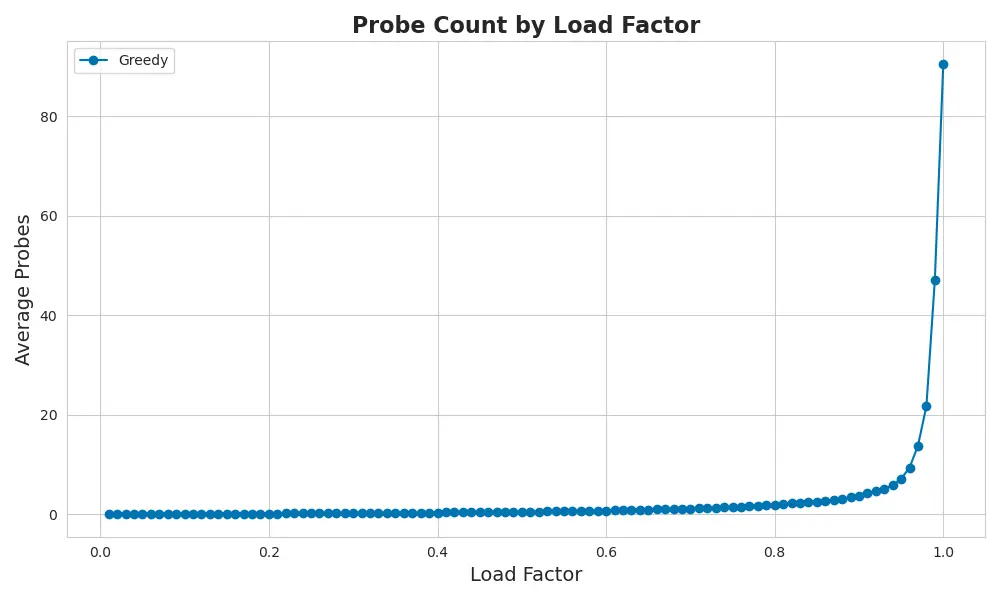
Greedy performs well early on — but probe cost spikes hard around 97% full.
For most of the journey, performance holds steady.
But just before the lot fills up, the probe cost spikes — sharp, unforgiving, and fast.
That’s the wall.
There’s no warning. No time to swerve.
One moment there’s room, the next you’re stuck doing loops. All it takes is a handful of new arrivals.
And that’s the real problem. Greedy doesn’t just fail — it fails suddenly.
Fallback can’t be a last resort. It has to shape how things fill up — and how they hold together under pressure.
From Cliffs to Curves
We aren’t just chasing performance. We’re chasing a different shape.
Greedy probing is like a single-level car park with one entrance and one row.
It works fine when there’s space. But as it fills up, everyone queues for the same few bays — and there’s nowhere else to go.
Elastic hashing changes that.
Instead of one long row, we split the table into subarrays.
Think of them as separate car parks — each with its own layout. Each one gives the driver a new set of bays to try.
One lot full? No problem. Try the next. And the next.
Fallback isn’t a last-minute workaround — it’s in the layout.
It’s no longer linear. It’s layered. Predictable. Spread out.
But just having more lots doesn’t solve the problem.
If every driver still wants bay #17, you’ve just got the same pile-up in four different places.
Structure helps.
But without variation — it’s still chaos, just in parallel.
Our First Try: Unbalanced + Unrotated
We tried an elastic fallback strategy where each driver got access to several car parks — but was told to try the same numbered bay in each one. Always starting at car park A.
It sounded fair. It failed spectacularly.
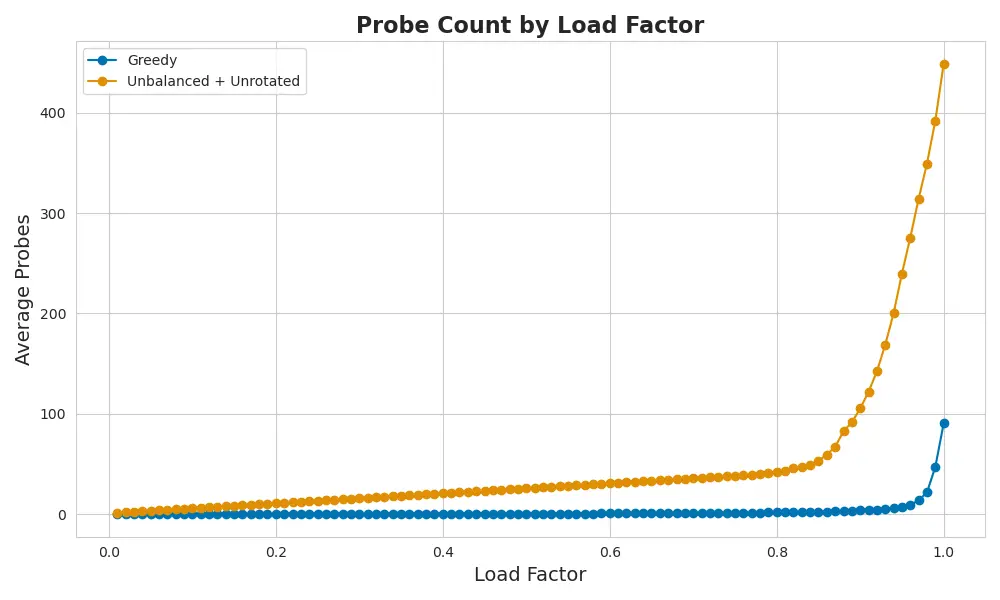
Unbalanced + Unrotated fallback performs worse than greedy — symmetry without variation leads to collisions.
It was worse than greedy.
Imagine four car parks — but every driver tries to park in bay #17.
That’s what unbalanced fallback does.
Each key gets four chances — but still aims for the same bay number every time.
If #17 is full in one lot, odds are it’s full in the others too.
It’s not fallback. It’s just four versions of the same bottleneck.
More car parks without variation just means more places to queue for the same spot.
We Rotated the Starting Car Park
So we tried giving each driver a different car park to start in.
It helped — a bit. Fewer pileups. A bit less circling.
But it still didn’t beat greedy.
let base = (hash as usize) % self.subarray_count;
for i in 0..self.subarray_count {
let subarray_idx = (base + i) % self.subarray_count;
}
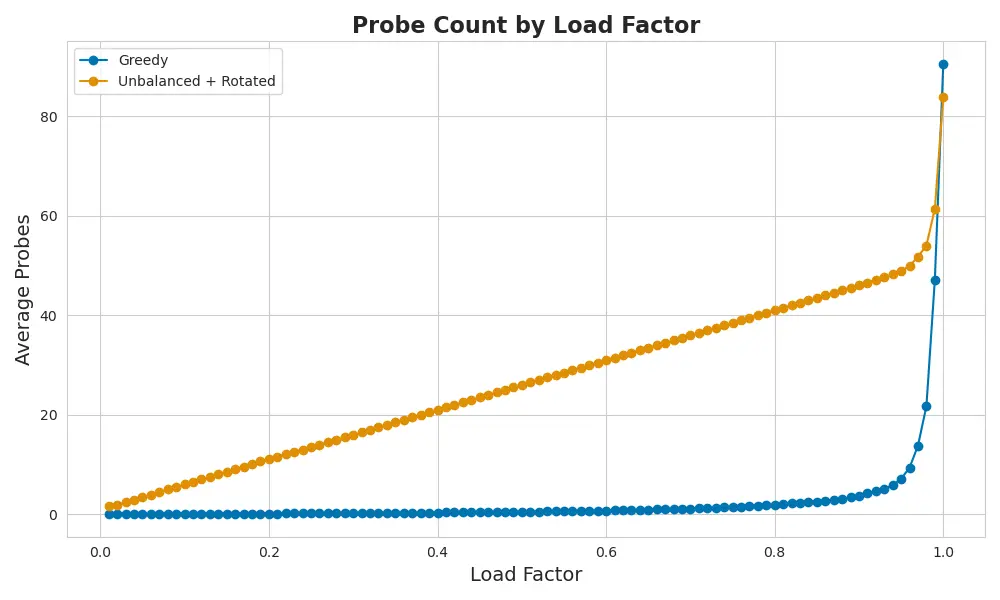
Rotating the fallback starting point reduces collisions slightly — but without slot variation, greedy still wins.
Why didn’t it work?
Because every driver still aimed for the same bay — they just entered from a different car park.
We changed the entrance, but not the destination.
Bay 17 in every lot still copped the full brunt of traffic.
Each driver pulls into a different car park — but still heads straight to the same bay number.
We spread out the arrivals. But not the demand.
And without that, rotation just delays the jam — it doesn’t prevent it.
Finally: Elastic Rotation
This is where everything clicked.
Balanced fallback doesn’t just rotate which car park a driver enters — it rotates the map inside each one.
Same driver. Same parking attendant. But in each car park, they’re handed a different set of instructions.
That means less crowding. Fewer pileups. No more stampede to bay #17.
Each fallback lot now gives a different layout — and that breaks up hotspots.
Traffic spreads. Pressure drops. The curve softens.
Now fallback actually works.
And it all comes down to one small shift:
fn slot_index(&self, hash: u64, subarray_idx: usize) -> usize {
if self.balanced {
((hash.rotate_right(subarray_idx as u32)) as usize) % self.slots_per_subarray
} else {
(hash as usize) % self.slots_per_subarray
}
}
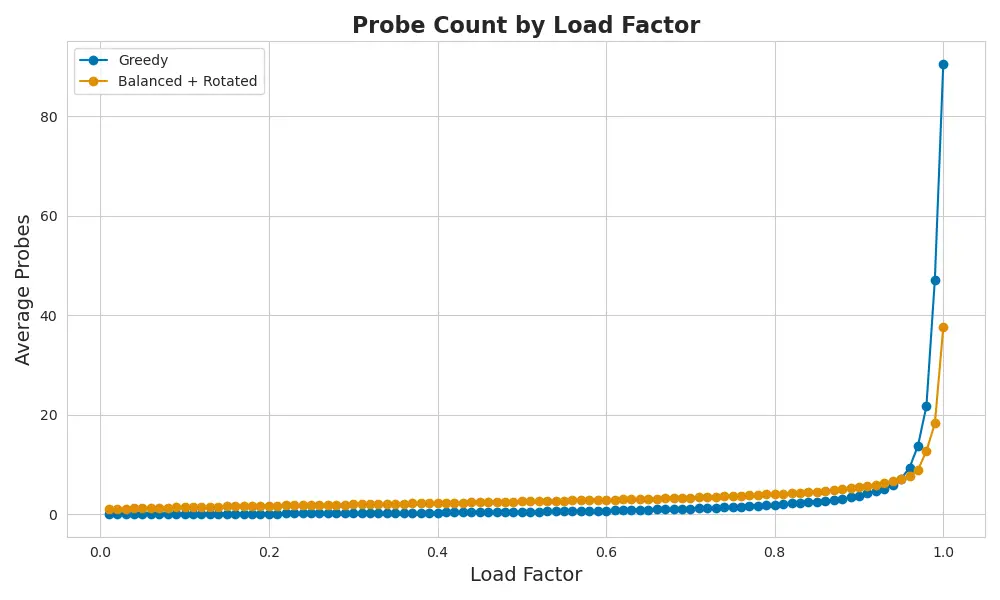
Elastic Rotation fallback spreads pressure evenly — and finally beats greedy under high load.
Now, every driver still wants a spot.
But instead of aiming for bay #17 in every car park, each attendant gives them a different route.
Rotation spreads where fallback starts.
Balance spreads what fallback targets.
And the result?
Not just fewer collisions — but a system that degrades predictably.
No more cliffs. Just a gentle hill
The Full Picture
Here’s how they all compare — now that you’ve seen the journey:
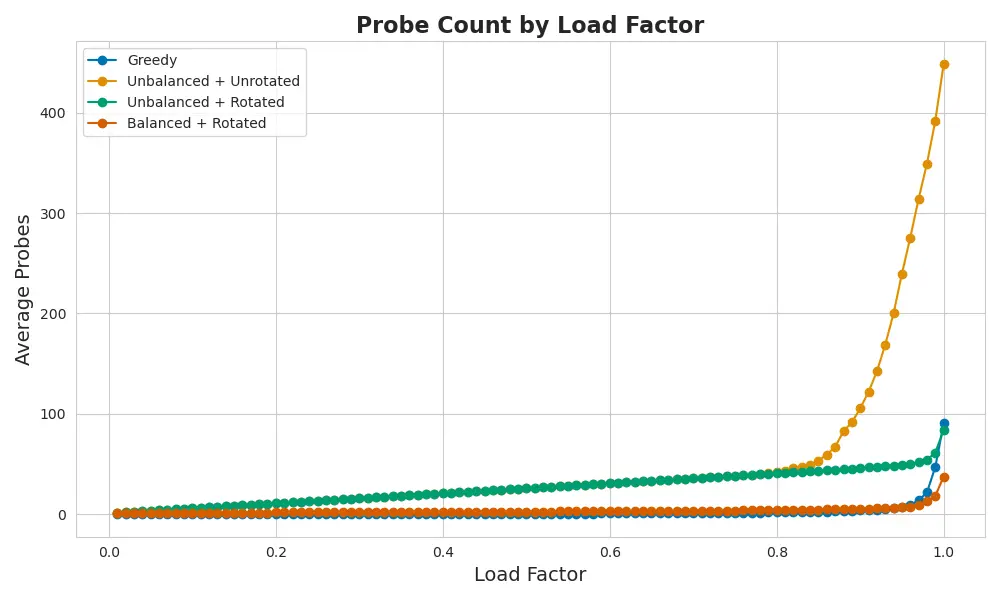
Greedy climbs quickly. But with rotation and balance, fallback stays smooth — even under pressure.
Elastic Rotation holds its shape. Every other variant — including greedy — buckles.
The Maths
The Maths Behind the Cliff
Greedy looks efficient — but its cost curve hides a trap:
$ \mathbb{E}[\text{probes}] = \frac{1}{1 - \alpha} $
Where \( \alpha \) is the load factor — the portion of the table that’s already full.
- At 80% full: ~5 probes
- At 90%: 10
- At 99%: over 100
You don’t get a gentle slowdown. You get a cliff.
Why? Because greedy fallback always checks the next bay. The fewer empty spots left, the longer that list of instructions gets.
It’s like trying to park at the beach on a public holiday — every turn is taken, and the attendant just keeps pointing you further down the row.
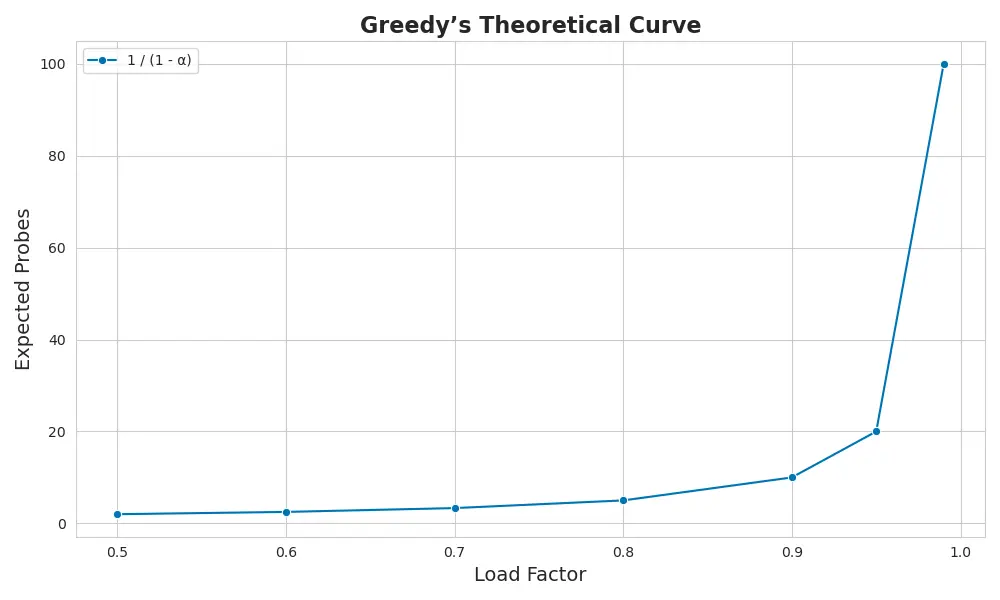
Greedy fallback performs well at low load — but climbs rapidly as the table fills.
This is why elastic hashing exists: to bend the curve. To leak pressure early, rather than explode late.
The Maths of Bounded Pain
Greedy’s cost curve spikes. But balanced fallback stays contained:
$ \text{max probes} \leq \mathcal{O}\left(\log \frac{1}{\delta}\right) $
Where \( \delta = 1 - \alpha \) — the remaining capacity in the table.
It doesn’t stop probe growth entirely. But it slows it down, flattens it out.
Instead of hitting a wall, you get a slow crawl.
Instead of being waved from bay to bay in panic, you ease through with time to think.
That’s what balanced fallback gives you:
A system that gives you warning, breathing room, and a fair chance at parking without stress.
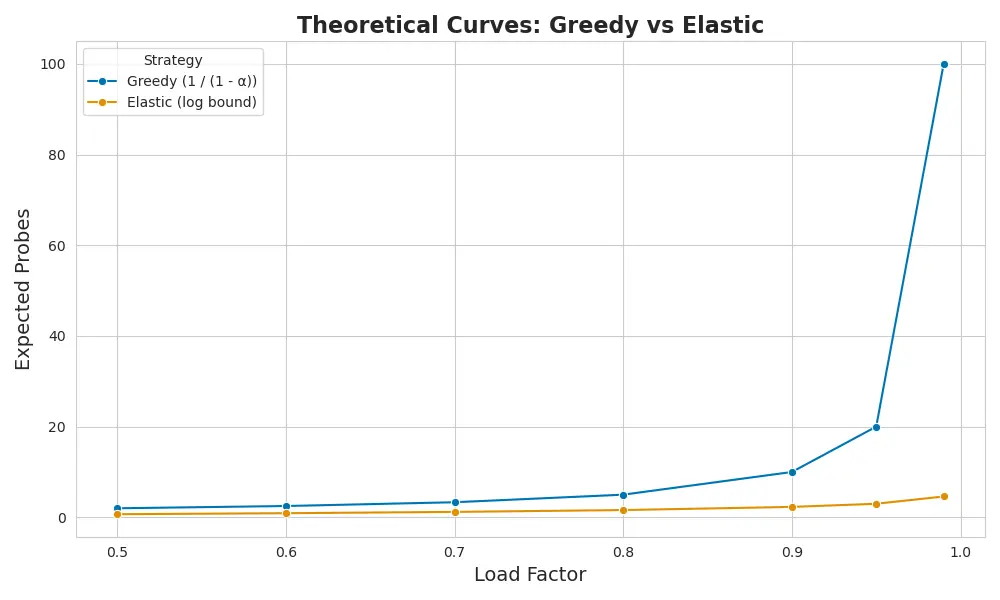
Elastic fallback bends early and stays flat — greedy climbs sharply as load increases.
Try It Yourself
Fire up the dev shell:
nix develop
Generate the plots:
just probes-at-load-post1
just probes-at-load-post2-unbalanced-unrotated
just probes-at-load-post2-unbalanced
just probes-at-load-post2-balanced
just plot-probes
All output lands in probe-data/, including the blog-ready charts.
Watch the wall.
Then watch it bend.
The Shape of Failure
You don’t build tables to sit half empty.
You build them to take load — to grow, stretch, and survive pressure.
And when that pressure hits, what matters isn’t peak performance — it’s behaviour.
How the system bends. How it breaks. How much warning it gives you.
Greedy gives you none.
It works — until it doesn’t. And when it breaks, it breaks fast.
That’s not just a system failure. It’s a human one.
We miss the warning signs. We normalise risk.
And when the spike hits — latency, cost, pressure — it feels sudden. But it isn’t.
The curve had flattened long before it broke.

Systems that fail like cliffs give no warning. Systems that fail like curves give you time.
That’s why fallback can’t be a patch. It has to shape how failure unfolds.
Elastic Rotation does exactly that.
By rotating the hash per fallback lane, it spreads load, breaks up collisions, and bends the curve early — before the system gets tight.
It’s not a trick. It’s a design shift. From fallback as emergency… to fallback as architecture.
Sometimes, resilience comes from the shape of the fallback — not its complexity.
Systems that fail gradually, not suddenly.
That hold their shape when pressure builds.
That’s the bound we came to break.
Next Up
We’ve bent the curve. Next, we build the full system.
Following the path laid out by Anshu, Dey, and Jayaram in Optimal Bounds for Open Addressing Without Reordering, we’ll go deeper — into fallback strategies that balance better and break a 40-year assumption.
Full probe logic. Batch-aware inserts. Search that stays fast, even when every bay’s nearly full.
